Houdini Black Magic

Table Of Contents

Black Magic Intro

This is honestly like stuff you should only whip out when trying to impress a honey u kno? This is all pretty poorly written, so please don’t bully me :(

ALL EXAMPLES IN THIS ARTICLE ARE AVAILABLE FOR DOWNLOAD ON MY GITHUB

Voodo #1 - Writing Vex With Python

SLAP DOWN A WRANGLE BOOYYYYYYYYYYYYY. It’s easy to miss that the VEXpression section of a wrangle is actually just a parameter like any string parameter, just thiccer. So like any string parameter, you can use hscript or python. Take a second and let that sink in, python.

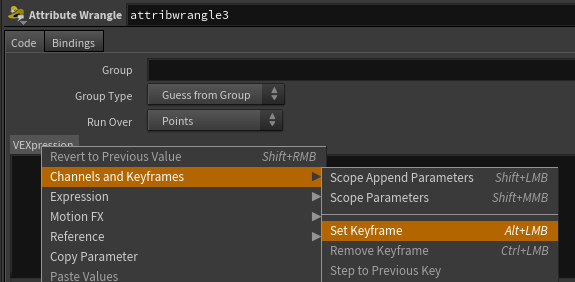
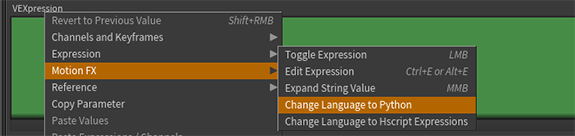
IN ANY TYPE OF WRANGLE right click your VEXpression parm, drop down a keyframe and set the vexpression language to python. BOOM we’re in. You’ll know it’s working because the text box will turn purple. Keyframe Set Py

Like any python expression you need to return your result. So any string we return that contains vex code will get executed by this parameter.

#define our functions
out = """
float aa(float i){ 
    return pow(i, 2); 
}
float ab(float i){ 
    return exp(i); 
}
float ac(float i){ 
    return sqrt(i);
} \n"""

#define our class suffixes
classes = "abc"

for class_name in classes:
    #create a new attribute with the class name and output
    #use .format() instead of % cuz that's the newer/sexier convention for string replacement.
    out += "@a{0} = a{0}(10);\n".format(class_name)

return out

You might be wondering what this example actually does on a practical level. To be completely honest, the above code literally does nothing of import, it’s more to show off the python-vex completion.

We’re basically using python to generate a few functions, and then we return a unique attribute based on the called function’s name!

This line specifically: out += "@a{0} = a{0}(10);\n".format(class_name) both chooses the function to call, and stores it’s value in a uniquely named attribute! Again, this is just outputting vex code, so if you click on the VEXpression parm, you’ll see the output vex! Neat!!!!!

Set Py

Though I can’t say the formatting is incredible on the output vex… ;)

Voodo #2 - Finding Prim Group Boundaries

This is gonna be a bit of a short entry as it’s a pretty straightforward effect. We’re going to write a quick snippet to find the boundary of a prim group.

If you’re unfamiliar with half-edges, I recommend you read my blog on splitting polygons here.

The algorithm can be described by these 5 simple steps:

  1. For all polygon’s, p1, in our mesh
    1. Find some starting half-edge, e1, and the group p1 belongs to.
    2. From e1, find all equivalent half edges.
    3. For each equivalent half edge, e2, find the prim, p2, that containins e2.
      • If p2 is not in the primgroup belonging to p1, mark our initial edge, e1, as a boundary.
      • Find the next edge in p1 and repeat until all prim edges contained by p1 been checked.

I’d really recommend trying to implement the process described above on your own, however if you’re lazy (yeah, I’m calling you out), I’ve written up a basic implementation below.

//this still goes in a prim wrangle
//selects the border of a prim group
void select_border_diff(string current_group; int primnum){
    int in_curr = inprimgroup(0, current_group, primnum);
    if(!in_curr) return;
    
    int h =  primhedge(0, primnum);
    int temp = h;
    do{
        int nb_prim = hedge_prim(0, hedge_nextequiv(0, h));
        if(!inprimgroup(0, current_group, nb_prim))
            setedgegroup(0, "border", hedge_srcpoint(0, h), hedge_dstpoint(0, h), 1);
        
        h = hedge_next(0, h);
    }while(h != temp);    

}
string a = chs("group_a");

int in_a = inprimgroup(0, a, @primnum);

select_border_diff(a, @primnum);

Voodo #3 - 2D Point Winding

I was recently tasked with this problem: Given a set of unordered points in the 2d plane (X,Z), find a method of building a coherent polygon (no overlaps) containing all points.

The easiest (and as I later learned most popular) method is to first find the average position of all the points in the set. From there we want to find the arc-tangent angle from each point position to the average position. We then want to sort our points based on these arc tangent values. And after sorting, the resulting polygon will be overlap free and totally coherent.

Why does this work? If the trigonometric tangent operator returns the slope of a line given an input angle, then the arc-tangent operator returns an angle, given the slope of a line. In our case we’re going to use the atan2() operator, which instead of taking in a slope, takes in the rise and run of our line, basically our X and our Y if we’re centered at the origin. Since our point set is not gaurenteed to be centered at the origin, we want to subtract off the average of our point set from our positions as a method of centering our point set. The angles returned by the arc-tangent then gives us the basis for which we can order our points as the angles are both unique, and for lack of a better word, wound about the point set’s center.

int pts[] = AN_ARRAY_OF_YOUR_POINTS;


vector pos[];
foreach(int pt; pts)
    append(pos, vector(point(0, "P", pt)));


vector cent = avg(pos);

float atan_test[];

//assuming it's 2d on the XZ axis
foreach(vector p; pos)
    append(atan_test, atan2(p.x - cent.x, p.z - cent.z));

int order[] = argsort(atan_test);
pts = reorder(pts, order);

addprim(0, "poly", pts);

I just want to point out that I am not the only person to solve this problem in this way, in fact it’s an ultra common solution. But regardless, it was one of those simple solves that made me feel like I was a dank mathematician when in reality im just a scared child. Hooray for math!

Voodo #4 - Point/Prim Removal Hot Tip

This is a very Houdini specific tip, however it’s something I run into enough that I felt it worth commenting on.

When solving a problem, removing points or prims is usually one of the slowest, if not THE slowest operation you can do, and should be avoided if possible.

If you do need to remove points, the fastest method is going to always be removing as much as possible in one call. Meaning the more spread out your deletions are, be it through a For-Each Block or inside of a Sop Solver, the slower your resulting program will be.

The Problem - Nearest Neighbor Pairs

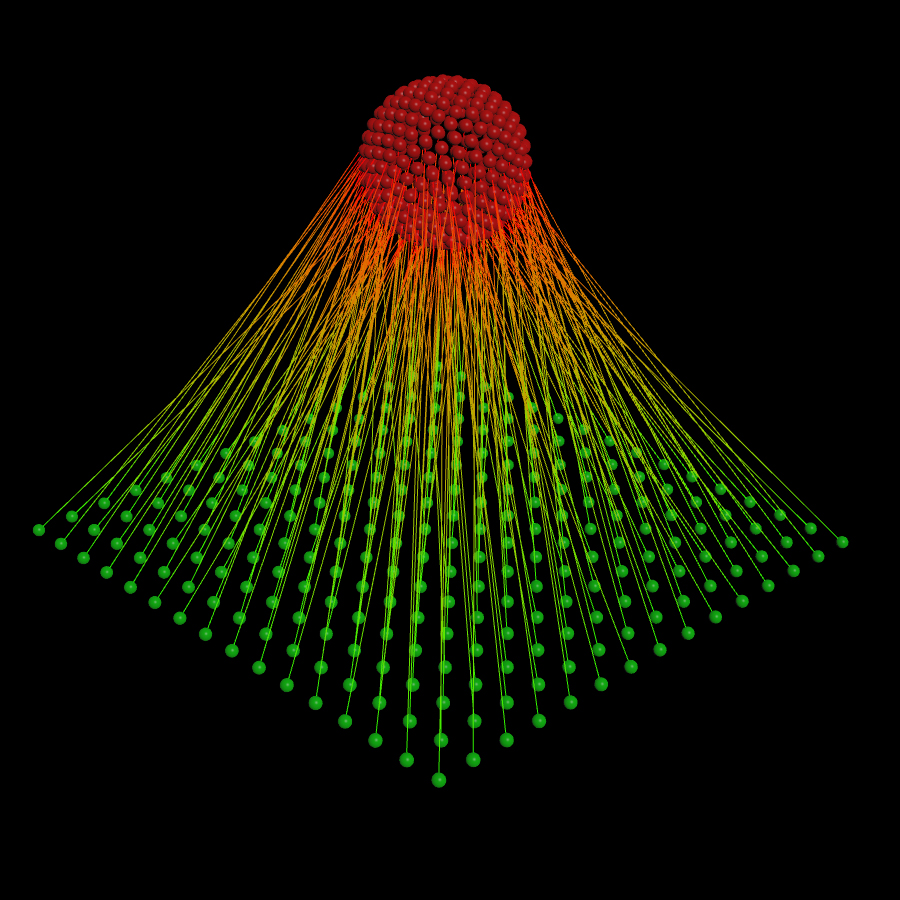
P2P Connections

Now again, I’m not saying you should never remove points, but let’s ponder a problem given to me by Adam Swaab, the problem of finding the nearest unique point from one point set to another. If the problem isn’t clear basically we want to find unique pairs of points between the two point sets, without overlaps. Adam initially sent me his file where had solved this problem and asked me if I knew how to make it run faster, as his solution took over a minute to find the pairs between two point sets each containing 15k points.

His solve was as follows:

Given two point sets A and B with the same number of points.

  1. Create a group __origpts and add all points in set A to this group.
  2. Create a group __availpts and add all points in set B to this group.
  3. Merge the two sets together.
  4. Create an attribute nearpt on the merged points for later storage.
  5. In a For-Each Block, in feedback mode where the iteration number is defined by the total point count:
    1. In a detail wrangle:
      • From the point, pt, who’s point number is equal to our current iteration number
      • Find the nearest point, avail_pt, in the group __availpts.
      • Set our nearpt attribute on pt, equal to avail_pt's point ID.
      • Remove the point, avail_pt

Or in vex form:

/*----------- DETAIL WRANGLE -----------*/
//input 0 is our points stream
//input 1 is our For-Each Block Meta-Data Node

int i = detail(1, "iteration", 0);

vector pos = point(0, "P", i);
int nearpt = nearpoint(0, "__availpts", pos);
int nearptid = point(0, "__nearptid", nearpt);
setpointattrib(0, "nearptid", i, nearptid, "set");
removepoint(0, nearpt);

This is a fine solution and solves the problem with no hickups, however the run time is really poor. If you think about it, not only is he looping 30 thousand times, doing 30 thousand nearpoints lookups, but he’s also removing 15 thousand points, in 15 thousand seperate calls.

Taking into consideration what I just said about removing points being costly (especially iteratively), doing it 15 thousand seperate times is going to absolutely destroy performance. So how do we speed this up? Hint: we get rid of all removepoint() calls.

Optomizing the Problem

Like we did before, let’s set this up in psuedo code to see how we’re going to tackle this without the use of removepoint().

The new solve can be described as follows:

Given two point sets A and B with the same number of points

  1. Create a group __origpts and add all points in set A to this group.
  2. Create a group __availpts and add all points in set B to this group.
  3. Merge the two sets together.
  4. Set a group on the merged set named __active which we’re going to leave empty for now.
  5. Create an attribute nearpt on the points for later storage.
  6. Create a detail attribute named orig_count with it’s value set to the number of points in the __origpts group.
  7. In a For-Each Block, in feedback mode where the iteration number is defined by the total point count:
    1. In a point wrangle, with it’s group mask set to __origpts:
      • find the nearest point in the group __availpts and write it’s index to the nearpt attribute.
    2. In a second point wrangle, with it’s group mask set to __availpts:
      • find the first point, f, in our geometry, who’s nearpt attribute is equal to our current point index.
      • Remove f from the __origpts group.
      • Add f to the __active group.
      • Remove our currrent point from the __availpts group.
    3. In a detail wrangle:
      • Set an attribute named stop equal to 1, if the number of points in the __active group is equal to the value of our orig_count attribute.
  8. In the For-Each Block End, set the stop condition equal to the detail attribute stop.
  9. Remove any point not in the __active group after the For-Each Block.

Again like always, this is the full vex code, broken up by which wrangle they should belong to.

/*----------- POINT WRANGLE #1 -----------*/
//GROUP MASK SET TO __origpts

i@nearpt = nearpoint(0, "__availpts", v@P);

/*----------- POINT WRANGLE #2 -----------*/
//GROUP MASK SET TO __availpts

int f = findattribval(0, "point", "nearpt", i@ptnum, 0);
if(f > -1){
    setpointgroup(0, "__origpts", f, 0);
    setpointgroup(0, "__active", f, 1);
    setpointgroup(0, "__availpts", @ptnum, 0);
}

/*----------- DETAIL WRANGLE -----------*/

i@stop = npointsgroup(0, "__active") == i@orig_count ? 1 : 0;

The final thing is how I’d like to add, is how we exit the For-Each Block early. On the End-Block itself, we’re going to add in a spare parameter (go up to the gear menu and click “Add Spare Parameter”), and drag the detail wrangle into that spare input. From here we’re going to set the Stop Condition parameter’s expression to this: detail(-1, "stop", 0). Which basically tells the End-Block to read the stop attribute from the wrangle, and if it’s equal to 1, stop the loop. The only reason we used a spare parameter for this is because we were too lazy to type out the relative path to the wrangle, but that would totally work too. Keep in mind that this loop IS NOT COMPILEABLE. It is important to keep in mind that compiling will not improve speed if you have to do a nearpoints lookup, as that operation gains no performance benefits from compiling as stated by Jeff Lait in the Compile-Block Master Class.

With this new algorithm, the pairing algorithm which took over a minute for 30k total points, has now been cut down to just over 1 second of total run time.

The reason it’s so much faster is due to, two major reasons. The first being that we’re not doing any point removal until after we’ve paired all the points, and the second being that we’re able to generate a lot of pairs in parallel rather than working on a single point per For-Each Block iteration.

Related

Contact